DIDÁCTICA DE LAS
MATEMÁTICAS
TRABAJO FINAL
DIDÁCTICA DEL ESPACIO Y LA GEOMETRÍA
ÍNDICE
PRIMERA PARTE: TEORÍA
- Introducción.
- ¿Por qué es tan
importante la geometría?
- Primeros pasos del
aprendizaje de la geometría.
- Aprender jugando
con la geometría en la escuela infantil.
- Objetivos.
-Tres tipos de espacios.
-Tres tipos de espacios.
SEGUNDA PARTE: ACTIVIDADES
EXPOSICIÓN
ANEXO: DIARIO
DE CLASE
CONCLUSIÓN FINAL
PRIMERA PARTE: TEORÍA
INTRODUCCIÓN
El
aprendizaje de la geometría en la etapa de Educación Infantil es muy importante
pues, según Chamorro (2005), los niños y las niñas nacen en un entorno
determinado con el que están en contacto y por ello, deben ser capaces de
realizar un esquema mental del espacio en el que se desarrollan. De esta
manera, el niño establece relaciones con el espacio y el entorno lo que le
produce una mayor seguridad para relacionarse con el mundo que le rodea,
modelizar los conceptos geométricos básicos, formar el pensamiento lógico
matemático y poder desarrollarse correctamente.
El
aprendizaje de la geometría, tradicionalmente, se ha basado en el desarrollo
lógico el cual tenía como única referencia el contenido de los libros de la
obra de Euclides, denominada Elementos. En esta obra se exponía las pautas
correspondientes para desarrollar el método axiomático.
Euclides,
planteó la geometría, a partir de quince axiomas. Sin embargo, el axioma más
relevante es el quinto postulado, que dice así por un punto pasa una paralela a
una recta dada y solo una. En la práctica escolar es común que estos
aprendizajes se memoricen sin tener en cuenta su comprensión.
Sin
embargo, con la instauración de las “matemáticas modernas” la geometría dejo de
ser tratada como un aspecto fundamental en los centros escolares. Diferentes
miembros educativos, consideraban que la geometría euclidea, era una materia
muerta, haciendo que esta sea poco interesante en los distintos niveles
curriculares. Por ello, los aprendizajes de los números y las operaciones son
mucho más relevantes.
Al
igual, hemos de tener en cuenta los acuerdos educativos que tomaron todos los
países occidentales tras la segunda guerra mundial. En ellos, se decidió dar
preferencia al álgebra, para la reconstrucción de la industria en Europa frente
a otros aprendizajes matemáticos.
¿POR
QUÉ ES TAN IMPORTANTE LA GEOMETRÍA?
El
aprendizaje de la geometría en las primeras edades tiene mucha importancia, y
ésta se produce en todos los ambientes educativos.Ante esto nos cuestionamos,
¿Cuál es el motivo primordial para considerar el aprendizaje de la geometría
como un aspecto importante?
El
primer motivo es que la geometría ayuda a los niños desde edades tempranas a la
construcción del pensamiento espacial.
El
procesamiento de la información se puede construir de dos formas distintas
según el hemisferio cerebral.
El
hemisferio central izquierdo, exactamente, el levohemisferio,
proceso la información en forma de pequeños códigos o palabras. Este
levohemisferio constituye el centro del lenguaje e incluye la
lectura-escritura.
Hemos
de destacar que la recepciones y descripciones de las situaciones visuales se
hacen de manera hablada o escrita. La actividad de este hemisferio controla el
procesamiento de la información en el nivel abstracto de palabras y lenguaje.
El
niño que posee una prevalencia levohemisférica domina muy bien las operaciones
de desarrollo secuencial, también utiliza el lenguaje para resolver sus
primeras investigaciones.
El
hemisferio derecho, denominado, dextrohemisferio,
su comportamiento es totalmente diferente al hemisferio izquierdo. Este
hemisferio procesa la información basándose en imágenes, es decir, trata
informaciones espaciales y visuales. Dicha información se trata desde un
aspecto global.
El
dextrohemisferio, es el centro de la intuición y de la creatividad. En este se
memorizan los hechos, que el niño registra visualmente, y se comunica a través
de imágenes y acciones.
Nuestra
sociedad otorga gran importancia a las actividades levohemisféricas. Porque es
más importante expresar acciones o creaciones a partir de palabras que a partir
de imágenes.
El
niño/a que tenga una gran capacidad y destreza espacial, tendrá un componente
primordial para la construcción del pensamiento matemático. Debido a que,
dispondrá de habilidades espaciales que les permitan realizar cálculos mentales
y reflexivos, cálculo numérico mediante imágenes, y podrá prever cualquier
problema.
PRIMEROS
PASOS DEL APRENDIZAJE DE LA GEOMETRÍA
Para
la elaboración del currículo geométrico en las primeras edades se debe de
partir de la comprensión por parte del alumnado del espacio que le rodea, a
través de la exploración de sus principales aspectos geométricos.
APRENDER
JUGANDO CON LA GEOMETRÍA EN LA ESCUELA INFANTIL
Desde
que nacen los niños están constantemente descubriendo y explorando la realidad
que les rodea, para ellos, este hecho es una necesidad. Mediante la cual,
perciben a través de los sentidos las percepciones espaciales de las
características geométricas de los objetos cotidianos de su entorno más
próximo.
Los
maestros y maestros deben propiciar actividades de aprendizajes, en las cuales
los niños apliquen sus percepciones interiorizadas en experiencias anteriores
y, de esta forma, provoca su evolución intelectual.
La
geometría forma parte de nuestro lenguaje matemático y, por tanto, es útil para
observar y percibir la realidad que nos envuelve. Eso sí, la geometría necesita
para ser elaborada o representada gráficamente al lenguaje plástico. Estos dos
lenguajes se interrelacionan y complementan para facilitar la concepción global
del área de lenguajes e intercomunicación (fundamental en educación infantil)
OBJETIVOS
Al
igual que el resto de contenidos, las matemáticas aparecen reflejadas en el
Real Decreto 1630/2006 del 29 de Diciembre del 2006 en el que se establece el
currículo de Educación Infantil en el que se fijan los objetivos, fines y
principios generales relativos a esta etapa. Estas se incluyen en el área de
conocimiento del entorno en la que se plantean entre otros, los siguientes
objetivos en relación con las mismas:
-
Observar y explorar de forma activa su entorno físico, natural y social,
desarrollar el sentido de pertenencia al mismo, mostrando interés por su
conocimiento, y desenvolverse en él con cierta seguridad y autonomía.
-
Indagar el medio físico manipulando algunos de sus elementos, identificando sus
características y desarrollando la capacidad de actuar y producir
transformaciones en ellos.
-
Representar atributos de elementos y colecciones, y establecer relaciones de
agrupamientos, clasificación, orden y cuantificación, iniciándose en las
habilidades matemáticas.
Y se
especifican los contenidos que se deben de trabajar; todos ellos agrupados en
el bloque 1 de dicha área: “Medio físico: elementos relaciones y medida”:
- Los objetos y materias presentes en el
medio, sus funciones y usos cotidianos. Interés por su exploración y
actitud de respeto y cuidado hacia objetos propios y ajenos y cuidado de
los mismos.
- Percepción de semejanzas y diferencias
entre los objetos. Discriminación de algunos atributos de objetos y
materias. Interés por la clasificación de elementos. Relaciones de
pertenencia y no pertenencia.
- Identificación de cualidades y sus
grados. Ordenación gradual de elementos. Uso contextualizado de los
primeros números ordinales.
- Cuantificación no numérica de
colecciones (muchos, pocos). Comparación cuantitativa entre colecciones de
objetos. Relaciones de igualdad y de desigualdad (igual que, más que,
menos que).
- Estimación cuantitativa exacta de
colecciones y uso de números cardinales referidos a cantidades manejables.
Utilización oral de la serie numérica para 7 contar. Observación y toma de
conciencia del valor funcional de los números y de su utilidad en la vida
cotidiana.
- Exploración e identificación de
situaciones en que se hace necesario medir. Algunas unidades
convencionales y no convencionales e instrumentos de medida. Aproximación
a su uso. Interés y curiosidad por los instrumentos de medida.
- Estimación intuitiva y medida del
tiempo. Ubicación temporal de actividades de la vida cotidiana. Detección
de regularidades temporales, como ciclo o frecuencia. Observación de
algunas modificaciones ocasionadas por el paso del tiempo en los elementos
del entorno.
- Situación de sí mismo y de los objetos en el espacio. Posiciones relativas. Identificación de formas planas y tridimensionales en elementos del entorno. Exploración de algunos cuerpos geométricos elementales. Nociones topológicas básicas (abierto, cerrado, dentro, fuera, cerca, lejos, interior, exterior...) y realización de desplazamientos orientados.
Además se plantean una serie de criterios
de evaluación de los que cabe destacar el que mayor relación presenta con las
matemáticas: Mostrar curiosidad e interés por el descubrimiento del
entorno, y, progresivamente: identificar, discriminar objetos y elementos del
entorno inmediato y actuar sobre ellos; agrupar, clasificar y ordenar elementos
y colecciones según semejanzas y diferencias ostensibles; discriminar y
comparar algunas magnitudes y cuantificar colecciones mediante el uso de la
serie numérica.
TIPOS DE ESPACIOS:
Según
la visión del niño sobre el espacio, podemos dos visiones: espacio cercano y
conocido y espacio lejano y desconocido.
El
espacio conocido también se conoce como espacio propio o inmediato; el niño
toca y experimenta sobre su propio cuerpo a través del movimiento corporal, con
las manos, pies, la vista,etc.
El
espacio lejano o desconocido se centra en la perspectiva, orientación y la
trayectoria, que para el niño son conceptos más abstractos y que irá
construyendo a lo largo de su vida.El aprendizaje sobre el espacio debe ir
formándose en sus mentes progresivamente, formando un todo, partiendo siempre
de su propio cuerpo a través de su propia experiencia y exploración. Cuando un
niño comienza a entender la percepción espacial, será capaz de reconocer y distinguir
los diferentes estados en los que se encuentran los objetos, como por ejemplo,
saber situar y distinguir un objeto que está encima de la mesa o al lado.
A
continuación, se explicará los tres espacios :
Es
indispensable que los docentes sean conscientes y conozcan las características
de los tres tipos de espacio derivados de los tres tipos de geometría que
explican las relaciones espaciales, ya que, gracias a estos conocimientos, los
docentes pueden utilizar estrategias de enseñanza para que los alumnos aprendan
a ubicarse en el espacio.
Para
trabajar esto vamos a explicar primero la diferencia entre los tres tipos de
espacios: espacio topológico, espacio proyectivo y espacio euclídeo.
ESPACIO
TOPOLÓGICO
El
reconocimiento, la representación gráfica de acercamientos, separación, orden,
entorno y continuidad son experiencias que se encuentran dentro del espacio
topológico. Las figuras sufren alteraciones que dan lugar al cambio de los
ángulos, de la longitud, las proporciones y del volumen. No obstante, a pesar
de estos cambios hay propiedades geométricas que permanecen invariables como,
por ejemplo, las relaciones espaciales de proximidad o acercamiento, la
separación entre puntos, el cierre de un contorno, la secuencia, la continuidad
o discontinuidad de líneas, superficies o volúmenes, se conservan en las
transformaciones topológicas.
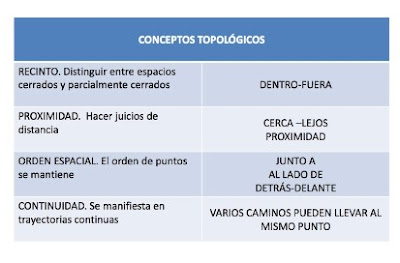
Para
comprender el espacio topológico, es importante mencionar algunos aspectos de
éste. Vamos a empezar hablando del recinto. El recinto, es la capacidad con la
que se pueden distinguir espacios completamente cerrados de espacios cerrados
parcialmente.
La
separación, es otro aspecto que destacar. Consiste en tratar relaciones
parte-todo haciendo diferencias en ilustración-entorno. La proximidad es la
capacidad para hacer referencia a la distancia y hacer juicios sobre esta. Esto
incluye la comprensión de relaciones como “cerca”, “lejos”, “al lado de”,
“junto a”
El
orden espacial: es la capacidad para mantener la secuencia y la dirección al
realizar una disposición lineal de 5 objetos o más, utilizando un conjunto
idéntico de objetos.
La
continuidad: es la capacidad de ver el espacio como un espacio continuo de
manera que varios caminos dan lugar al mismo punto.
ESPACIO
PROYECTIVO
“Las
preguntas que se hicieron los pintores mientras trabajaban en las matemáticas
de perspectiva ocasionaron que ellos mismos y, más tarde, los matemáticos
profesionales, desarrollaran la materia conocida como geometría proyectiva.
Esta rama, la creación más original del siglo XVII es ahora una de las
principales de las matemáticas” (Kline, 1997; 237)
Los
pintores del Renacimiento y otros autores de etapas anteriores tenían la
necesidad de hacer representaciones cada vez un poco más realistas, alejadas
todas ellas de los prototipos religiosos de la sociedad de la época. Para ello,
hicieron uso de los puntos, las líneas y figuras geométricas para plasmar en
sus obras, principalmente, en sus cuadros, la profundidad y el espacio. Es así,
como se incorpora al mundo del arte los principios y leyes de las matemáticas,
la perspectiva enriqueció la proyección de realismo natural en los lienzos de
este periodo histórico.
El
espacio proyectivo abarca la representación de transformaciones en las cuales
las longitudes y los ángulos experimentan cambios, los cuales dependen de la
posición relativa entre la fuente que lo plasma y el objeto representado. Este
tipo de representación tiene como objetivo plasmar el objeto representado lo
más real posible, no obstante, su proyección es relativa.
Por
ejemplo, un paisaje, la representación de este dependerá de múltiples factores:
· La distancia de observación.
· Del ángulo visual.
Aspectos
muy relevantes a la hora de observar y comprender representaciones de un mismo
objeto o escena.
Las
transformaciones proyectivas pueden ser de tres tipos:
· Isométricas: se pueden llamar también
movimiento. Son aquellas que conservan las medidas de los ángulos y de los
segmentos de la figura original y su transformada (giro, translación y
simetría).
· Isomórficas: son aquellas que
conservan las formas. Entre dos figuras transformadas se puede establecer
relaciones de proporcionalidad (semejanza y homotecia).
· Anamórficas: son las transformaciones
que no conservan las formas (afinidad y homología).
En
una transformación proyectiva observamos que la representación de los puntos
sigue siendo puntos; las líneas siguen siendo líneas; los ángulos siguen siendo
ángulos; sin embargo, la magnitud de los ángulos y las longitudes de las líneas
cambian en función de la posición relativa del objeto representado o de la
perspectiva.El tamaño y la forma de las figuras no se conserva tras la
transformación proyectiva. La línea recta es proyectiva porque se mantiene tras
una transformación. Los ángulos, la distancia entre puntos, la
perpendicularidad y el paralelismo si se modifican, por lo que tampoco son
espacios proyectivos.
Otras
propiedades como la proporcionalidad entre áreas y líneas se mantienen invariables
durante una transformación proyectiva, es decir, a pesar de esta, se pueda
reconocer las estructuras geométricas que componen al objeto representado.
EL ESPACIO EUCLÍDEO
El
espacio euclídeo o métrico estudia y representa las longitudes, ángulos, áreas
y volúmenes como cualidades que persisten en las figuras aunque sean sometidas
a transformaciones rígidas. Las transformaciones euclídeas consisten en
movimientos rígidos en el plano horizontal o vertical, traslaciones y giros.
Son de rotación y traslación.
Rectas
paralelas, perpendiculares o figuras geométricas son todos espacios euclídeos.
¿Qué
espacios geométricos y perpendiculares no se modifican con las transformaciones
euclídeas?
Se
mantiene la distancia entre puntos, el ángulo y el paralelismo, la
perpendicularidad, la recta, forma de figuras y la distancia que es lo más
importante.
Distancia entre puntos:
Magnitud
escolar que mide la relación de lejanía entre dos puntos. Se trata de la
distancia existente entre un punto u objeto A y un punto u objeto B.
La
distancia entre dos puntos coincide con la longitud del camino más corto entre
dos puntos.
Rectas
paralelas:
Se
encuentran siempre a la misma distancia, una de la otra, pero nunca se tocarán.

· Ángulos:
Se
trabajará el espacio a través de la realización de ángulos realizados con el
propio cuerpo (cuarto de vuelta, media vuelta y vuelta completa).
· Rectas perpendiculares:
Se
trata de rectas que se juntan en ángulos rectos

· Propiedades
del cuadrado:
Es el polígono que tiene sus lados opuestos paralelos y,
por tanto, es un paralelogramo. Dado que sus 4 ángulos internos son rectos.
Cada ángulo interno de un cuadrado mide 90 grados, y la suma de todos ellos es
360º. Está formado por 4 lados y 4 vértices que conforman los ángulos.
·
Propiedades otras figuras
geométricas:
Trabajar lados y vértices de
otras figuras diferentes al cuadrado como pueden ser el triángulo y el círculo.
-Circulo: es
una figura geométrica sin lados ni vértices.

-Triángulo:
está formado por 3 lados y 3 ángulos que varían según el tamaño de las líneas y
según el tipo de ángulos. Todos los triángulos tienen 3 vértices.
- Rectángulo:
está formado por 4 lados, iguales entre sí de dos en dos. Sus 4 ángulos son de
90º. Para dibujar el rectángulo hay que saber, que tiene dos lados iguales
largos y dos cortos, también iguales entre sí, 4 ángulos iguales y 4 vértices.
-
Pentágono: figuras geométricas con más de 4 lados. Sus lados
no son iguales y está compuesto por 5 lados que conforman sus 5 vértices.
SEGUNDA PARTE: ACTIVIDADES EXPOSICIÓN
ESPACIO TOPOLÓGICO
1. DENTRO-FUERA



Vídeo:
1. DENTRO-FUERA
Descripción y objetivos: La seño diseñará un circuito con círculos. En la primera estación los niños y niñas tendrán que ir saltando dentro de los círculos con los dos pies juntos y pasando de un círculo a otro. En la segunda estación los niños tendrán que ir saltando en zig-zag de manera que vayan cayendo una vez dentro y otra vez fuera de los círculos para seguir avanzando. En la tercera estación los niños deberán saltar con los dos pies juntos dentro de los círculos y luego con los dos pies separados por fuera del círculo. A la misma vez que van saltando tendrán que ir diciendo si están fuera o dentro de los círculo. Al principio de cada estación habrá un mapa en forma de explicación que les ayudará a realizar el recorrido. De esta forma los niños y niñas irán interiorizando el concepto de dentro-fuera, para poder aplicarlo en su vida diaria y para poder adaptarse con más facilidad al entorno que le rodea. Trabajarán el concepto topológico de “recinto”, distinguiendo entre espacios cerrados y parcialmente cerrados y ampliando sus conocimientos sobre los conceptos de dentro y fuera.
Materiales y recursos: Hemos utilizado las cuerdas para construir los círculos y folios de papel en los que aparecen impresas las guías de cada estación. La clase se ha dividido en tres grupos que han ido rotando por las estaciones de tal forma que todos los niños y niñas han ido pasando por cada una de ellas
Vídeo:
2. PROXIMIDAD
(CERCA-LEJOS)
Soy Laura María Sarrias Arrabal y mi
trabajo trata sobre el espacio topológico, más en concreto, sobre la
proximidad. Como han defendido autores como Piaget, con la proximidad, los
niños desarrollan la capacidad para hacer juicios de distancia utilizando bien
su propio cuerpo, o bien objetos relacionados entre sí en un espacio y una
distancia determinada. Para poder llevar a cabo este desarrollo, será
importante que los niños tengan una representación mental del espacio y
relacionen los objetos mediante los conceptos de cerca y lejos.
Por ello,
he diseñado dos actividades para que este aprendizaje se produzca de forma
natural mediante el juego. Una actividad es una maqueta en la que los niños
deberán colocar un muñeco cerca o lejos de un objeto determinado en un espacio
familiar para ellos, como es el aula, y la otra, es un juego, en el que se
utiliza como espacio la clase, donde a través del propio cuerpo y la ayuda de
los compañeros deberán buscar piezas de un puzle utilizando conceptos como frio
y caliente.
ACTIVIDAD 1: "NUESTRA CLASE ES LA MEJOR"
El
juego consiste en poner un muñeco cerca o lejos de los objetos que hay en la
maqueta, utilizando la ruleta para ver qué objeto es. Tendremos unas tarjetas
que servirán para saber si el muñeco tiene que estar cerca o lejos del objeto
que nos haya tocado en la ruleta. La tarjeta que tenga una cruz representará el
cerca y la tarjeta que esté en blanco, representará el lejos.
Seguidamente,
haremos dos equipos de 10 personas por cada equipo, además, habrá 1 persona que
será el juez, que se encargará de anotar los puntos de cada equipo y el resto
será jurado para ver si algunos de nuestros compañeros hacen trampa y
comunicárselo a nuestro juez.
Un
equipo será el color azul y otro el morado, y competirán entre ellos, para ver
quien coloca antes el muñeco.
En
cada equipo, habrá 5 parejas, una de las personas de la pareja girará la ruleta
y cogerá la tarjeta y la otra moverá el muñeco colándolo donde nuestra pareja
nos indique. Ambos equipos girarán las ruletas a la vez y ganará un punto quién
coloque el muñeco antes. Finalmente, ganará el equipo que tenga más puntos
conseguidos.
Para la realización de esta maqueta he utilizado cartón, pinturas, papel impreso y cola. Dicha maqueta la he elaborado por mi misma y aunque ha sido un poco laborioso, con la ayuda de la profesora sería una tarea ideal para que los niños puedan llevarla a cabo ellos mismos y desarrollen competencias como la creatividad o el trabajo colaborativo, entre otras. Además, servirá para familiarizarse con el entorno educativo en el que están inmersos todos los días.
Para la realización de esta maqueta he utilizado cartón, pinturas, papel impreso y cola. Dicha maqueta la he elaborado por mi misma y aunque ha sido un poco laborioso, con la ayuda de la profesora sería una tarea ideal para que los niños puedan llevarla a cabo ellos mismos y desarrollen competencias como la creatividad o el trabajo colaborativo, entre otras. Además, servirá para familiarizarse con el entorno educativo en el que están inmersos todos los días.
A continuación, adjunto el vídeo de la realización de la actividad en clase:
ACTIVIDAD 2: "BUSCAMOS EL PUZLE"
https://www.youtube.com/watch?v=ZBchvkiKhL0&t=1s
ACTIVIDAD 2: "BUSCAMOS EL PUZLE"
El
juego consiste en esconder piezas de puzle en la clase para después con la
ayuda de los compañeros encontrarlas y formar el puzle.
Para
ello, nos dividiremos en dos grupos, cada grupo se dividirá, a su vez, en dos
partes, una parte se quedará en la clase conmigo y la otra saldrá fuera de la
clase. Las personas de ambos grupos que se queden dentro de la clase, deben
esconderle las piezas del puzle al equipo contrario y ver donde esconde el
equipo contrario sus piezas. Utilizando el frío para las cosas lejanas y el
caliente para las cercanas, les diremos a los compañeros de nuestro grupo que
se quedaron fuera, dónde están las piezas que ha escondido el equipo contrario.
Cuánto más difícil se lo pongamos mejor, ya que ganará el equipo que antes
forme el puzle.
Para la realización de esta actividad he utilizado cartón, imágenes adaptadas a la edad de los niños y pegamento. Para que el puzle tuviese la forma real de un puzle con una consistencia rígida, pegué las imágenes a un cartón del mismo tamaño que éstas y, más tarde, recorté en pequeños trozos las imágenes para que así los niños pudiesen buscarlas para formar finalmente el puzle.
Para la realización de esta actividad he utilizado cartón, imágenes adaptadas a la edad de los niños y pegamento. Para que el puzle tuviese la forma real de un puzle con una consistencia rígida, pegué las imágenes a un cartón del mismo tamaño que éstas y, más tarde, recorté en pequeños trozos las imágenes para que así los niños pudiesen buscarlas para formar finalmente el puzle.
A continuación, adjunto el vídeo de la realización de la actividad en clase:
https://www.youtube.com/watch?v=EJRsXYjVCbg&feature=youtu.be
ESPACIO PROYECTIVO
2. IZQUIERDA-DERECHA
Título de la actividad: “Aquí y allí estará”
Desarrollo de la actividad:
El aula se dividirá en 2 grupos de 15 alumnos cada uno, y a su vez estos formarán parejas entre sí. El alumno que quede suelto ejercerá de árbitro de la actividad. Los demás irán saliendo por parejas, situándose uno frente a otro y cada uno de ellos con una maqueta.Una vez situados uno frente al otro comenzará el juego. Este juego consistirá en que uno de los dos integrantes de la pareja será elegido por el árbitro como capitán que deberá empezar a situar a los integrantes de su granja como a él más le guste. En la realización de cada movimiento, su pareja, que debe permanecer atenta, deberá ir colocando sobre su maqueta los mismos objetos y en el mismo lugar, de manera que al final queden elaboradas dos maquetas totalmente idénticas.
El árbitro se situará al lado de ellos con una señal en la mano donde por un lado tendrá un círculo verde, el cual levantara cual la pareja acierte, y por el otro un círculo rojo, el cual levantará cuando estos se equivoquen. Los demás integrantes del grupo ejercerán de jurado y contarán con una tabla de resultados donde irán anotando los puntos obtenidos por cada pareja. Los puntos se anotarán con un gomet verde si la maqueta se realizó correctamente, y con un gomet rojo si hubo errores en su realización. Al final de la actividad se contarán los gomet de cada equipo y ganará la partida aquel grupo que más gomets verde haya conseguido.
Objetivos:
- Introducir al niño en los conceptos izquierda/derecha.
- Trabajar el espacio proyectivo mediante el sentido de la vista.
Recursos:
- Humanos: docente y alumnos
- Espaciales: aula
- Espaciales: aula
- Materiales: 4 maquetas, objetos para colocar en las maquetas, paleta o señal de indicaciones, tabla de resultados, gomets rojos y verdes y 2 silvatos.
Temporalización.
Se realizarán 3 sesiones a la semana de unos 30 minutos aproximadamente.
Esquema lógico-matemático:
Con esta actividad se trabajara el espacio proyectivo a través del sentido de la vista y la utilización de maquetas mediante las que trataremos de proyectar un espacio real en el que se situarán objetos claramente observables por los niños y niñas. Esto acercará a los niños/as a los conceptos de izquierda/derecha los cuales trabajándose poco a poco serán capaces de llegar a dominar.
Actividad planteada por: Inmaculada Fátima Alba Cáceres.
Video de la realización de la actividad:
Actividad planteada por: Inmaculada Fátima Alba Cáceres.
Video de la realización de la actividad:
LA LÍNEA RECTA
UN VIAJE A CASA DE ABUELA
Soy Leticia Estébanez Vera y he realizado una actividad
denominada “Un viaje a casa de abuela”, mediante la cual he trabajado el
concepto de línea recta.
En
primer lugar, explicaré los materiales que he elaborado y utilizado para
realizar el juego. Un gran mural en el cual está dibujada la casa de la
abuelita, frutas realizadas con gomaeva y tizas de colores, así como, medallas
para caracterizar a los más pequeños de lobos o Caperucitas rojas.
La actividad ha sido realizada en la terraza exterior de
las aulas del Aulario, donde importamos clases de matemáticas. Inicialmente en
asamblea contamos a los niños el cuento infantil de Caperucita Roja .
Posteriormente, simularán que son Caperucita Roja, todos caracterizados con la
medalla de dicho personaje, y se pondrán en marcha para llevar a su abuelita un
cesto con alimentos. El camino que deben recorrer por el bosque estará marcado
con una línea de cinta aislante roja o una línea de tiza en el suelo, que
deberán ir pisando desde el punto de partida hasta el de llegada. Un requisito
indispensable es que no podrán dejar de ver la casita de su abuelita en ningún
momento.
En un primer momento, todos los alumnos serán Caperucita, uno tras otro en fila deberán hacer el recorrido hasta su abuelita. En la segunda ronda, unos alumnos jugarán con un rol de lobo y otros de nuevo con el rol de Caperucita, en función de las medallas que posean. Los lobos, pintarán en el suelo con tizas caminos alternativos que no sean rectos, para que Caperucita no pueda llegar a casa de la abuelita y darle su cesto de frutas. Durante el camino los lobos intentarán entretener a Caperucita para desviarla de su camino, ofreciéndole más frutas o convenciéndola de que por el camino que el sabe llegará antes a su destino, por ejemplo. Ante ello, las Caperucitas, han de quedarse muy quietas y seguir en línea recta hasta llegar a su abuelita. Sino es así, estas se convertirán en un lobo.
 |
En dicha actividad se trabajará el espacio proyectivo, reforzando así la orientación y la posición de una forma lúdica a partir de un camino que parte de un punto de salida y otro punto de llegada, es decir, coordinando distintas posiciones en el espacio. El niño o niña fundamentalmente, desarrollará y trabajará el concepto de línea recta, es decir, el desplazamiento en el espacio procurando siempre una misma dirección. La docente durante la actividad en todo momento recordará, que para llegar a sus destinos, en este caso la casa de la abuelita, no han de perderla de vista, siempre su mirada tiene que estar fija en ella.
A continuación, la demostración práctica de mi actividad en clase:
ESPACIO EUCLÍDEO
1. ÁNGULOS
1. ÁNGULOS
Título de la actividad: “Muévete”
Desarrollo de la actividad:“TRABAJAR
EL ESPACIO CON LOS ÁNGULOS”
Cada
niño deberá seguir con los ojos vendados un recorrido que estará dibujado en el
suelo del aula con cinta aislante. Otro compañero le irá dando indicaciones
para completar el recorrido con las siguientes instrucciones: media vuelta
(180º), cuarto de vuelta(90º) y vuelta completa sobre sí mismo (360º).
Previamente, en clase, hemos trabajado los ángulos con señales, dibujos y
actividades sencillas que le han facilitado su aprendizaje. El docente introducirá
los conceptos de las señales de tráfico para que los niños/as lo conozcan e interactúen
con ellos, por ello, las señales de tráfico simbolizan la vuelta completa,
media vuelta y cuarto de vuelta para colocarlas en el lugar del recorrido donde
proceda.
Objetivos:
- Introducir al niño en los conceptos de
cuarto de vuelta, media vuelta y vuelta entera.
- Introducir al niño a los conceptos de las
señales de tráfico.
- Trabajar el espacio euclideo mediante el
sentido de la vista.
- Manejar el espacio a través de los ángulos.
Recursos:
Ø Humanos: docente y alumnos
Ø Espaciales: aula
Ø Materiales:
- Cinta aislante.
- Lazos.
- Señales de Tráfico.
Temporalización.
Se
realizarán 2 sesiones a la semana de unos 20 minutos aproximadamente.
Esquema lógico-matemático:
Trabajaremos el espacio euclídeo a través de los ángulos.
Trabajaremos el espacio euclídeo a través de los ángulos.
Con
esta actividad se trabajara el espacio euclídeo a través del sentido de la
vista y del tacto, por ello, utilizaremos las señales de tráfico mediante las
que trataremos de proyectar un espacio real
en el que se situarán los niños/as que deberán realizar un recorrido.
Esto acercará a los niños/as a los conceptos de cuarto de vuelta, media vuelta
y vuelta completa, los cuales trabajándose poco a poco serán capaces de llegar a
dominar completamente.
Actividad planteada por: Ana Osorio Mendez
Video de la realización de la actividad:
Video de la realización de la actividad:
2. DISTANCIA ENTRE PUNTOS
El
objetivo de esta actividad es trabajar la distancia entre puntos de manera
fácil y divertida, haciendo participes a todos los alumnos. En primer lugar,
vamos a dividir la clase en 8 grupos de 4 personas cada uno y a cada grupo le
corresponde una figura geométrica. Para hacer los grupos, pondremos 4 cajas y
dentro de cada caja, habrá pequeñas figuras geométricas (en total hay 8 figuras
geométricas distintas) y de cada figura hay 4 piezas iguales que corresponden
al total de miembros de cada grupo. Estas 8 figuras geométricas son: circulo,
cuadrado, triangulo, rectángulo, trapecio, rombo, pentágono y romboide. De
manera que, dentro de la caja habrá mezclados: 4 círculos, 4 triángulos, 4
rectángulos, etc. En una de las piezas de cada figura geométrica vendrá escrito
la palabra juez. El juez de cada grupo participará en el diagrama y los 3
miembros restantes participarán en el papel continuo. De manera más explícita,
un miembro de cada grupo lanzará su figura geométrica sobre el papel continuo y
la pegará con el gomet para que no se mueva. Después los otros dos
participantes medirán con la cuerda de colores la distancia a la que ha llegado
el objeto y trazarán una línea. Medimos contando los colores de la cuerda
(mientras más colores, más distancia) El juez, se encargará de poner en el
diagrama los colores de la cuerda en relación con la distancia obtenida.
Gracias a ello, podremos ver con mayor precisión la distancia que ha obtenido
la figura de cada grupo al ser lanzada. Finalmente, un alumno de la clase será elegido
para responder dos preguntas sobre la actividad escritas en el diagrama, para
que reflexionen sobre los conceptos trabajados.
Los
alumnos para realizar esta actividad, usarán diferentes materiales como por
ejemplo, una cuerda de colores que podrán pintar y realizar ellos mismos usando
los colores que deseen. Un papel continuo gigante, el cual estará dividido en 8
partes relacionadas con las 8 figuras geométricas y un diagrama que puede ser
también confeccionado por los alumnos. Las figuras geométricas que son
lanzadas, pueden ser hechas a mano por los alumnos o si disponen de ello,
pueden utilizar figuras de plástico o de cualquier otro material.
Se
pueden realizar variantes de la actividad dependiendo del número de alumnos que
participen en ella, añadiendo más figuras geométricas para lanzar y más colores
en la cuerda para medir.
ANEXO: DIARIO DE CLASE
TEMA 7: DIDÁCTICA DEL ESPACIO Y LA GEOMETRÍA
En
este tema queremos saber cómo el niño domina el espacio, y para trabajar eso lo
vamos a ver a través de tres tipos de espacios: espacio topológico, espacio
proyectivo y espacio euclídeo.
ESPACIO
TOPOLÓGICO
Se
reparten globos, se inflan un poco sin hacerle un nudo y se dibuja algo en
éstos. Nos fijamos en cómo ha quedado y, posteriormente, lo seguimos inflando y
le hacemos un nudo. El dibujo con respecto al principio es igual, aunque el
globo sea más grande.
TRANSFORMACIÓN
TOPOLÓGICA, es cuando puedes estirar algo sin
romperse se dice que se ha aplicado una transformación topológica. Tanto inflar
como comprimir es una transformación.
¿Qué
significa estudiar el espacio a través de las transformaciones?
Si
nosotros cogemos una transformación del tipo que sea, nos fijamos en las cosas
que no varían y los conceptos, ideas que se conservan es lo propio de ese
espacio.
Según
eso, nosotros anteriormente hemos hecho una transformación topológica, y nos
vamos a centrar en un globo en las cosas que no ha cambiado, no ha cambiado
exterior e interior (corazón con ojos dentro). Éstos son aspectos y conceptos
del espacio topológico, es decir, la idea de dentro y fuera.
También la idea de región (dos regiones, la que está dentro del corazón y la
que está fuera) y frontera (línea del corazón, por mucho que estires de sigue
manteniendo la línea). Asimismo, aparece la idea de arriba/abajo.
Una
cosa importante es la proximidad, (está al lado de, junto a…) son
ideas del espacio topológico, ejemplo, un ojo está próximo a otro, tú lo
estiras y sigue existiendo esa proximidad. Otro concepto es la continuidad,
que una línea sea continua tú la estiras y sigue siendo continúa.
ACTIVIDAD
2. Hacer un dibujo de la pared del aula (dibujo topológico:
no guardo la distancia exacta entre el corcho y el perchero, etc.; no guardo el
tamaño exacto entre el bolso y el perchero, etc. Sin embargo, si guardo la
cercanía, etc.
Cualquier
dibujo que hagamos es una representación topológica de la realidad.
El
primer espacio que los niños dominan es el espacio topológico, y eso se pone de
manifiesto en los dibujos.
EQUIVALENCIAS
TOPOLÓGICAS
La línea recta no es un
concepto topológico, porque si se transforma no mantiene sus cualidades porque
puede ser curva. Las figuras cerradas si son topológicas.
ESPACIO
PROYECTIVO
Durante
las transformaciones proyectivas se conservan las proyecciones de objetos, los
recorridos de usa y vuelta y por último, la plasmación en un cuadro de un
espacio real. Todo ello, son espacios proyectivos, es decir, los distintos
puntos de vista que varias personas pueden contemplar de una misma realidad.
Pero,
¿Qué aspectos geométricos y espaciales no se modifican?
El
único aspecto geométrico o espacial que no se modifica durante una
transformación proyectiva, y que por tanto es proyectivo, es la línea recta.
Otros aspectos como el tamaño y forma de las figuras, los ángulos,
el paralelismo, la perpendicularidad o la distancia entre puntos se modifican
durante las transformaciones proyectivas y por tanto, no pertenecen al
espacio proyectivo.
Los
niños dominan el espacio proyectivo, si son capaces de tener en cuenta todos
los puntos de vista que se puede tener acerca de una realidad.
Los
conceptos que son fundamentales en dicho espacio proyectivo son:
• Izquierda
y derecha: coordinar distintas posiciones en el espacio.
• Línea
recta: seguir una misma dirección.
Estos
son algunos ejemplos de espacios proyectivos:
EL
ESPACIO EUCLÍDEO
Las
transformaciones euclídeas consisten en movimientos rígidos: traslaciones y
giros. Son de rotación y traslación.
Rectas
paralelas, perpendiculares o figuras geométricas son todos espacios euclídeos.
¿Qué
espacios geométricos y perpendiculares no se modifican con las transformaciones
euclídeas?
Se mantiene la distancia
entre puntos, el ángulo y el paralelismo, la perpendicularidad, la recta, forma
de figuras y la distancia que es lo más importante.
ESPACIO EUCLÍDEO
| |
Distancia entre puntos
|
Medida de longitud
|
Rectas paralelas
|
Las distancias son constantes
|
Ángulos
|
Cuantificar dirección.
|
Rectas perpendiculares
|
Ángulo recto.
|
Propiedades del cuadrado
|
Vértices, lados
|
Propiedades otras figuras geométricas
|
Vértices, lados.
|
ACTIVIDADES
DIDÁCTICA DEL ESPACIO Y LA GEOMETRÍA
ACTIVIDAD
1: RECINTO (DENTRO-FUERA)
En
esta actividad los niños deberán dibujar en sus camisetas en dibujo. Después,
esta camiseta se la pondrá otro compañero y los niños que han dibujado las
camisetas, cada uno deberá identificar la suya. De esta forma, si un niño
dibuja en su camiseta un círculo con un corazón dentro, deberá identificarla
sabiendo que el dibujo sigue siendo el mismo.
ACTIVIDAD
2: PROXIMIDAD CERCA-LEJOS
En
esta actividad sesionarán pelotas diferentes en el espacio (golf, baloncesto,
fútbol…), y también se situarán los niños en el espacio. A continuación, la
docente hará preguntas; ¿Qué pelota está más cerca de la de baloncesto?, ¿Qué
niño está más lejos de la pelota de tenis?, etc.
ACTIVIDAD
3: ORDEN ESPACIAL: JUNTO A, AL LADO DE, DETRÁS-DELANTE
1.
Los niños bailan al compás de la música. Cuando la docente pare la música, los
niños deberán pararse y comentar a quién tienen al lado, detrás, delante…
2.
Realizar búsquedas para dominar el espacio. Por ejemplo; la docente dice a un
niño: trae el libro de matemáticas que está al lado de la mesa.
ACTIVIDAD
4: CONTINUIDAD: VARIOS CAMINOS PUEDEN LLEVAR AL MISMO PUNTO
Construir
un laberinto con varios caminos hacia un punto de salida en el que tengan que
coger el camino continuo.
ACTIVIDAD
5: COORDINAR DISTINTAS POSICIONES EN EL ESPACIO (DERECHA-IZQUIERDA)
Cada
niño posee una maqueta. Uno de los niños sitúa en su maqueta una serie de
elementos y otro de sus compañeros debe ponerlos en la misma posición, pero en
su maqueta, la dificultad irá aumentando. Por ejemplo, distanciado las maquetas
o añadiendo muchos más elementos.
ACTIVIDAD
6: LÍNEA RECTA: SEGUIR UNA MISMA DIRECCIÓN
Inicialmente
en asamblea contamos a los niños el cuento infantil de Caperucita Roja.
Posteriormente, simularán que son Caperucita Roja y se pondrán en marcha para
llevar a su abuelita un cesto con alimentos. El camino que deben recorrer por
el bosque estará marcado con una línea de cinta aislante roja en el suelo que
deberán ir pisando desde el punto de partida hasta el de llegada, no podrán
dejar de ver la casita de su abuelita en ningún momento.
En
un primer momento todos los alumnos serán Caperucita a, uno tras otro en fila
deberán hacer el recorrido hasta su abuelita. Después, unos alumnos jugarán con
un papel de lobo y otros de nuevo de Caperucita. Durante el camino los lobos
intentarán sacar a Caperucita del camino, ante ello los niños han de quedase
muy quietos y seguir en línea recta hasta llegar a su abuelita. Sino es así,
está se convertirá en un lobo.
ACTIVIDAD
7: DISTANCIA ENTRE PUNTOS (MEDIDAD LONGITUD)
Los
niños saltarán desde una línea. Tras esto medirán la distancia a la que han llegado.
En lugar de utilizar unidades de medida usaré una cuerda de colores, los cuales
indiquen la distancia.
En
un papel continuo se dibujará las medidas con distintos colores para comparar
quién ha llegado más lejos y hacer un diagrama de barras. Algunos niños
participarán saltando y otros lanzando algún objeto.
ACTIVIDAD
8: RECTAS PARALELAS (LA DISTANCIA ES CONSTANTE)
Construir
unas vías del tren. Para ello, se disponen palos de diferentes tamaños, para
que puedan construir las vías, deben coger los palos a la vez que tengan el
mismo tamaño, para que las líneas sean paralelas.
ACTIVIDAD
9: ÁNGULOS (CUANTIFICAR DIRECCIÓN)
En
esta dirección los niños harán un recorrido por parejas (uno hará de ciego y
otro de guía) cada vez que llegue a una esquina, su guía deberá decirle cuanto
tiene que girar (un cuarto de vuelta, media vuelta etc)
ACTIVIDAD
10: RECTAS PERPENDICULARES
En
esta actividad, se disponen bolos y se hacen varios caminos desde la salida
hasta donde se encuentran, pero solo un camino es perpendicular y los demás son
horizontales. De esta forma, los niños tienen que razonar que solo la recta
perpendicular es la que te permite derribar los bolos.
ACTIVIDAD
11: PROPIEDADES DEL CUADRADO (VÉRTICES, LADOS ETC)
1.
Esta actividad consta de una gymkana con tres fases. En la primera hay un
cuadrado con una cartulina donde los niños tienen que colocarse para formarlo.
En la segunda, hay figuras geométricas que tienen que colocar para formar el
cuadrado (por ejemplo, dos triángulos) en la tercera deben formar un cuadrado,
pero esta vez sin la guía de la cartulina en la que aparece dibujado el
cuadrado.
2.
En una bolsa con diferentes figuras geométricas, los niños tienen que reconocer
mediante el tacto de que figuras se trata. Si, por ejemplo, no tiene vértices,
se trata de un círculo, si contiene varios vértices es un cuadrado etc.
3.
Dentro del aula, reconocen donde hay figuras geométricas.
ACTIVIDAD
12: PROPIEDADES DE OTRAS FIGURAS GEOMÉTRICAS (VÉRTICES, LADOS ETC)
Comparar
dos figuras geométricas. Reconocer cuadrados y rectángulos en el aula. Tras
esto, buscar las diferencias entre las figuras. Después se hacen dos grupos y
se juega a la figura oculta. Uno le tiene que preguntar a otro una sola
pregunta para adivinar de qué figura se trata. Por ejemplo, ¿tiene los lados
del mismo tamaño? Y si responden que sí, ya saben que se trata de un cuadrado.
Finalmente, se hace un registro para saber qué grupo ha adivinado más.
CONCLUSIÓN FINAL
Tras
la elaboración de este trabajo hemos descubierto la gran importancia que tiene
la geometría y el espacio en nuestra vida diaria desde el momento en que
nacemos. Además, por nuestra propia experiencia podemos decir que en la
actualidad este tema no se toma, ni se trabaja con la importancia que en
realidad tiene para la futura vida cotidiana de los niños y niñas. Básicamente,
la mayoría de los docentes se empeñan con tratarlo centrándose únicamente en
enseñar a los niños/as a distinguir entre varios tipos de figuras geométricas
como pueden ser el círculo, el triángulo y el cuadrado, sin tener en cuenta
objetos reales y cercanos a los niños/as con los que se podrían trabajar muchos
de los conceptos que engloba la geometría y el espacio, y que pueden despertar
en estos un mayor interés y motivación a la hora de aprender.
Desde
edades tempranas, el proceso de enseñanza-aprendizaje de la geometría, debería
llevarse a cabo a través de la manipulación, la exploración y la propia
experiencia, ya que esta resulta ser la manera más válida para que un niño/a
interiorice el conocimiento de manera adecuada.
De
acuerdo con Mequè Edo, es mucho más adecuado “comenzar la aproximación a la
geometría con un tratamiento intuitivo y exploratorio del espacio y de los
objetos que nos rodean” (Edo, M. (1999), p.54) El conocimiento geométrico no
puede ser adquirido a través de información dada por el docente, sin que los
alumnos sean partícipes de su propio aprendizaje, puesto que si la mente del
alumno no se encuentra implicada, no podrán desarrollarse verdaderos
aprendizajes.
Para
conseguir desarrollar en los alumnos un auténtico conocimiento geométrico, son
necesarios tres pasos, de acuerdo con Mª Antonia Canals (1997):
1º
Explorar el espacio: Los niños necesitan de la experiencia para poder construir
aprendizajes reales, que no estén basados solamente en la información que
alguien le ofrezca. Desde que nacen, todo lo que aprenden lo hacen a través de
la observación del entorno que les rodea. Por ello, es importante que en los
centros escolares fomentemos esta forma de aprender.
2º
Comparar los elementos observados: Está claro que no podemos quedarnos sólo en
la exploración, ya que de ser así no se conseguiría el conocimiento geométrico,
porque tampoco inducimos a los niños a razonar. Deben comparar aquello que ven,
que manipulan; para poder establecer relaciones.
3º
Expresar verbalmente aquello que han observado y las acciones realizadas para
poder interiorizar el conocimiento.
Si
nos ponemos a pensar en nuestro entorno actual y nuestra propia experiencia,
vemos que realmente estamos rodeados de objetos, formas, diseños y
transformaciones desde el momento en que nacemos por lo que desde la más
temprana infancia estamos experimentando directamente (aunque sea de manera
inconsciente), con las formas de los objetos y
los movimientos de los mismos. Con esto podemos ver claramente como las propiedades geométricas son cada vez más
accesibles y presentes en la vida cotidiana, cultural y técnica de nuestros
días. Gradualmente vamos tomado posesión del espacio, orientándonos, analizando
formas y buscando relaciones espaciales de situación, de función o simplemente
de contemplación, por medio de la intuición.
Por
lo tanto, podemos decir que como futuros docentes para la correcta enseñanza de
la geometría y el espacio deberemos llevar a cabo una metodología activa y
lúdica, y no podremos cometer el error de ofrecer a los alumnos objetos que
poco tengan que ver con su entorno cercano, sino que deberemos saber aprovechar
aquellos juguetes, utensilios y objetos cotidianos y familiares cercanos a
estos, de manera que logremos tener activo su interés y podamos aumentar su
curiosidad por conocer el mundo. En definitiva, deberemos proporcionar un
aprendizaje activo y basado en el interés
de los propios niños/as.
Por
nuestra propia experiencia podemos decir que en la actualidad el tema del
espacio y la geometría no se toma ni se trabaja con la importancia que este
tiene para la futura vida cotidiana de los niños y niñas. Básicamente la
mayoría de los docentes se conforman con tratarlo centrándose únicamente en
enseñar a los niños a distinguir entre varios tipos de figuras geométricas como
pueden ser el círculo, el triángulo y el cuadrado dejando de lado conceptos
mucho más importantes que deberían de ser trabajados.
BIBLIOGRAFÍA
Romero Salvador, A. (2014). La Geometría en la etapa de
Educación Infantil. (Trabajo
de Fin de Grado, Universidad de Almería). Recuperado de: http://repositorio.ual.es/bitstream/handle/10835/3610/1412_Trabajo%20de%20Fin%20de%20Grado.pdf?sequence=1
Fernández Barrio, S. (2013). La comprensión del espacio en
Educación Infantil. (Trabajo
de Fin de Grado, Universidad de la Rioja). Recuperado de: https://biblioteca.unirioja.es/tfe_e/TFE000686.pdf
Castillo Quintero, L.,
Ibarra Zavala, A., Monsiváis García, A., Montalvo Ortiz, R. & Morales
Tovías, V. (2007). Longitud de
un segmento y distancia entre dos puntos. (Colegio
de Bachilleres del Estado de Tamaulipas). Recuperado de: https://es.slideshare.net/guest34fbd2/tema-2-longitud-de-un-segmento-y-distancia-entre-dos-puntos
Martínez Villar, E.M. Descubriendo la Geometría en
Educación Infantil. (Trabajo
de Fin de Grado, Universidad de Valladolid) Recuperado de: https://uvadoc.uva.es/bitstream/10324/3982/1/TFG-G%20354.pdf
Briales Marín, M., Dueñas
Gil, A., Gallardo Muñoz, T. & González García, M. Didáctica del espacio, el tiempo y
la Geometría en la Educación Infantil. Recuperado de: http://es.calameo.com/read/004641469c0aed51d31e8
Estrada Berlanga, I. (2012).
Figuras geométricas y su clasificación. Figuras
y cuerpos geométricos. Recuperado
de: https://figurasycuerposgeometricos.wordpress.com/que-son-las-figuras-geometricas/
Calvo, X. (2002). La geometría: de las ideas del
espacio al espacio de las ideas en el aula. Barcelona:
GRAÓ.
Castro Bustamante, J.
(2004). El desarrollo
de la noción de espacio en el niño de Educación Inicial. Recuperado de http://www.saber.ula.ve/bitstream/123456789/171193/2/artículo5.pdf
Saunders, R, Bingham-Newman,
A.M. (1998). Perspectivas
piagetianas en la educación infantil. Madrid:
Ediciones Morata.
Alba Cáceres, I.F.,
Estébanez Vera, L., González Luque, J., Jiménez Alamilla, I., Osorio Méndez, A.
& Sarrias Arrabal, L.M. (2018). Tema 7: Didáctica del espacio y la
geometría. Didáctica de la
Matemática en la Educación Infantil. Recuperado de: http://didacticadematematicas3.blogspot.com.es/2018/01/didactica-de-las-matematicas-tema-7.html